扫描线
扫描线的原理,线段树优化扫描线。
扫描线
从直观上讲,扫描线算法就是拿一条线,扫过整个图形,从而计算出图形的周长或面积。
最经典的例子:平面上有很多个矩形,矩形的长宽要么平行于轴,要么平行于轴,矩形可以互相重叠,问这些矩形覆盖了多大的面积。
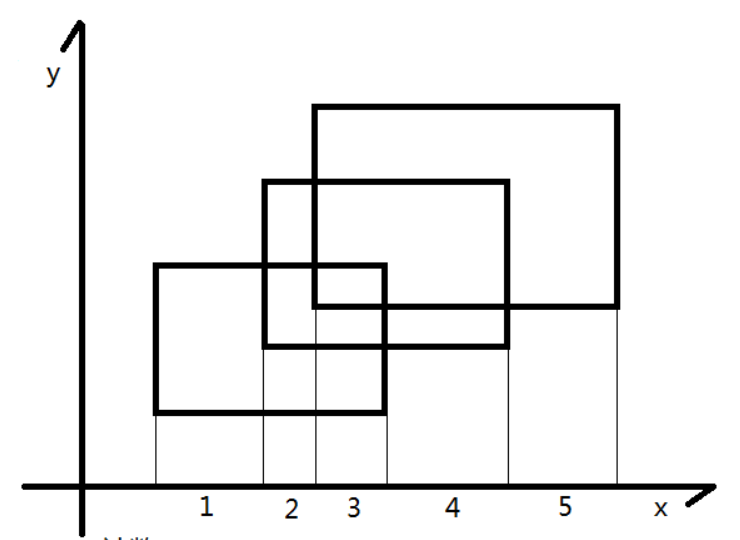
如图就是一组符合要求的矩形,假设我们要计算的就是这个的面积。
我们考虑用一条垂直于轴的直线,从所有矩形中最左边那条边开始向右移动,一直到最右边的那条边,则这条直线和被覆盖区域存在一些交点,并且在一定范围内,这些交点的纵坐标是不变的。例如,图中标注的横轴部分,在这一段移动直线的时候,纵向的覆盖始终是不变的,所以可以直接长宽去统计贡献。
接下来考虑到底在什么条件下纵向的覆盖长度不变。通过看图可以发现,每当扫描线经过一条矩形的垂直于轴的边的时候,覆盖就可能改变。具体来说,经过某个矩形的左边的时候,一般会增加覆盖(不增加可能是因为之前就覆盖过了),经过某个矩形的右边的时候,可能会减少覆盖(不减少可能是因为还有其他矩形在覆盖)。这样不变量以及变化时机就都找到了。
那么我们解决这个问题的扫描线算法就来了:
-
对于读入的矩形,分成两条线段存储其两条垂直于轴的边,标记是左边还是右边,这样会得到条边。
-
对边进行排序,保证等会儿扫描线是按照从左到右的顺序扫过的。
-
开一个统计纵向贡献的数组,初始化为全,从左到右枚举边
-
先计算一下刚扫过的部分的面积,具体来说是
(seg[i].x - seg[i - 1].x) * cnt,cnt表示贡献数组中不是的项数 -
如果是左边,则在相应的纵坐标范围增加的贡献(区间加)
-
如果是右边,则在相应的纵坐标范围减少的贡献(区间减)
-
最终答案就算出来了。
容易看出,在实现的时候存在两个问题:
- 如果真的按照纵坐标去修改贡献数组,无法处理超大值域以及浮点数,所以需要离散化。
- 修改和统计贡献可以使用线段树优化。
最基础的扫描线算法就是这样了。
基于本题给出不加优化的代码模板:
#include <bits/stdc++.h>
using namespace std;
const int N = 10010;
const int M = 10010;
typedef struct {
int x, y1, y2, flag;
} Seg;
Seg segs[2 * N];
int n, c[M], segcnt = 0;
void add_seg(int x, int y1, int y2, int flag) {
segs[++segcnt].x = x;
segs[segcnt].y1 = y1;
segs[segcnt].y2 = y2;
segs[segcnt].flag = flag;
}
bool cmp(const Seg &a, const Seg &b) {
return a.x < b.x;
}
int main() {
int x1, y1, x2, y2;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
add_seg(x1, y1, y2, 1);
add_seg(x2, y1, y2, -1);
}
sort(segs + 1, segs + segcnt + 1, cmp);
for (int i = segs[1].y1; i < segs[1].y2; i++) { // 注意边界
c[i] += segs[1].flag;
}
int ans = 0;
for (int i = 2; i <= segcnt; i++) {
int high = 0;
for (int j = 0; j < M; j++) {
if (c[j] > 0) {
high++;
}
}
ans += (high * (segs[i].x - segs[i - 1].x));
for (int j = segs[i].y1; j < segs[i].y2; j++) {
c[j] += segs[i].flag;
}
}
printf("%d\n", ans);
return 0;
}